Question

In right angle ABC, angle C is the right angle, AC = 3 and AB = 5. Point D is on hypotenuse AB, such that DB = 1. Find the area of the triangle DBC.

Answer 1

Look at the picture.

To find the area of triangle DBC we need to find its base, x, and its height, h.

Triangle ABC is a right triangle, so using the Pythagorean theorem we can find x.

`(\hbox{one leg})^2+(\hbox{the other leg})^2=(\hbox{the hypotenuse})^2 \\ 3^2+x^2=5^2 \\ 9+x^2=25 \\ x^2=25-9 \\ x^2=16 \\ x=√(16) \\ x=4`

Now look at triangles ABC and DBH. They both are right triangles and have the same angle α. That means they're similar and their corresponding sides are proportional. The ratio of the side opposite to angle α to the hypotenuse is the same in both triangles - so the ratio of h to 1 is the same as the ratio of 3 to 5.

`(h)/(1)=(3)/(5) \\ h=(3)/(5)`

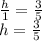
The base x is 4, the height h is 3/5. Calculate the area:


`A=(xh)/(2)=(4 * (3)/(5))/(2)=2 * (3)/(5)=(6)/(5)`

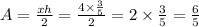
The area of triangle DBC is 6/5.