Question

The four points (−2, 5), (−2, −1), (6, −1), and (3, 5) are the vertices of a polygon. What is the area, in square units, of this polygon?

Answer 1

39 square units

Explanation:

Answer 2

Look at the picture.

The polygon is a right-angled trapezoid.

The area is:

`A=(a+b)/(2) * h`

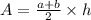
The points (-2,-1) and (6,-1) lie on the same horizontal line, so the distance between them is 6-(-2)=6+2=8. The length of a is 8 units.
The points (-2,5) and (3,5) lie on the same horizontal line, so the distance between them is 3-(-2)=3+2=5. The length of b is 5 units.
The points (-2,5) and (-2,-1) lie on the same vertical line, so the distance between them is 5-(-1)=5+1=6. The length of h is 6 units.


`A=(8+5)/(2) * 6=(13)/(2) * 6=13 * 3=39`

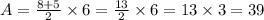
The area is 39 square units.