Question

How to combine fraction

Answer 1

`\Large \frac { x }{ y }`
`\begin{matrix} \rightarrow numerator \\ \rightarrow denominator \end{matrix}`


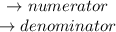
If two (or more) fractions have the same number as their denominator, you can just go ahead and add their numerators, without changing the denominator. For example:


`\frac { 1 }{ 2 }` and
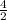
`\frac { 4 }{ 2 }` has the same number (2) as their denominator. So we will add their numerators, without changing the denominator.


`\frac { 1 }{ 2 } +\frac { 4 }{ 2 } \quad =\quad \frac { 1+4 }{ 2 } \quad =\quad \frac { 5 }{ 2 }`

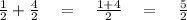
So we added the numerators (1 + 4 = 5) and kept the denominator same (2) and we got (
`(5)/(2)`

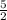
This was the case where the fractions' denominator was same. What if it's not ?

If their denominator isn't equal, we're gonna have to equalize them ourself. How to do that ?

Let's show it with an example :


`\frac { 1 }{ 2 }` and
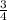
`\frac { 3 }{ 4 }` do no have the same number as their denominator. To be able to add them, we have to equalize their denominators.


`\frac { 1 }{ 2 }` 's denominator is 2 and
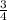
`\frac { 3 }{ 4 }` 's is 4

What can we do to equalize them ? Well, 4 is two times 2 (
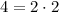
`4 = 2\cdot 2` ) So we cane multiply the denominator of
`\frac { 1 }{ 2 }` (which is 2) with 2 , to equal it to
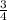
`\frac { 3 }{ 4 }` 's denominator (which is 4).

But, there is a catch here. When multiplying a fraction's denominator before adding it to another, you should make sure that you're preserving its ratio. What does that mean ?

Let's take the number
`\frac { 4 }{ 6 }`

(1) if we multiply only its numerator with a number (let it be 3)


`\frac { 3\cdot 4 }{ 6 } \quad =\quad \frac { 12 }{ 6 } \quad =\quad 2`

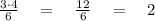
You got a new fraction with a different ratio than
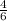
`(4)/(6)`. And it is also equal to 2, but
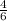
`(4)/(6)` isn't equal to 2.

(2) if we multiply only its denominator with a number (let it be 3 again)


`\frac { 4 }{ 3\cdot 6 } \quad =\quad \frac { 4 }{ 18 }`

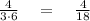
You got a new fraction again, with a different ration than
`(4)/(6)` .

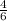
How can we know that ? Well, if you simplify these two numbers to the simplest number, you'll get a different fraction or integer. Let's do so.


`\frac { 4 }{ 6 } \quad =\quad \frac { 2\cdot 2 }{ 2\cdot 3 } \quad =\quad \frac { 2 }{ 2 } \cdot \frac { 2 }{ 3 } \quad =\quad 1\cdot \frac { 2 }{ 3 } \quad =\quad \frac { 2 }{ 3 }`

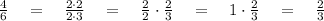
So the simplified form of
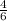
`(4)/(6)` in the fraction form is
`(2)/(3)`


`\frac { 4 }{ 18 } \quad =\quad \frac { 2\cdot 2 }{ 2\cdot 9 } \quad =\quad \frac { 2 }{ 2 } \cdot \frac { 2 }{ 9 } \quad =\quad 1\cdot \frac { 2 }{ 9 } \quad =\quad \frac { 2 }{ 9 }`

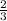
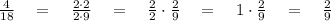
And the simplest form of
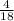
`(4)/(18)` as a fraction is
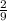
`(2)/(9)` , which is not equal to
`(2)/(3)`


`\frac { 2 }{ 3 } \quad \\eq \quad \frac { 2 }{ 9 }`

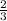
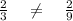
So what to do, to preserve the ratio ? Simle. We'll multiply also the numerator with the same number we're going to multiply the denominator with.

Let's get back to our example.

Adding
`\frac { 1 }{ 2 }` and
`\frac { 3 }{ 4 }`

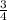
We were going to multiply
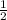
`(1)/(2)` 's denominator with 2. Now that we know, the ratio must not change, we'll also multiply the numerator with 2.


`\frac { 2\cdot 1 }{ 2\cdot 2 } \quad =\quad \frac { 2 }{ 4 }`

Now we've got a number which has the same denominator as
`\frac { 3 }{ 4 }`

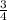
We can add them now,


`\frac { 2 }{ 4 } \quad +\quad \frac { 3 }{ 4 } \quad =\quad \frac { 2+3 }{ 4 } \quad =\quad \frac { 5 }{ 4 }`


`\boxed { \frac { 1 }{ 2 } \quad +\quad \frac { 3 }{ 4 } \quad =\quad \frac { 5 }{ 4 } }`

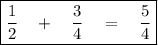
I hope this was clear, if not please ask and I'll try to explain.