Question

This graph shows two line segments whose endpoints are pairs of complex numbers. What are these two pairs? What complex number is common to both lines?

Answer 1

The common complex number to both lines is
`\(-(17)/(3) + (17i)/(3)\)`.

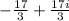Let's calculate the complex numbers corresponding to the endpoints of each line segment.

For the first line segment:

Endpoint 1: (-3, 3)

Endpoint 2: (4, -4)

The complex number corresponding to a point (a, b) in the complex plane is a + bi. Therefore:

Endpoint 1 corresponds to the complex number -3 + 3i.

Endpoint 2 corresponds to the complex number 4 - 4i.

For the second line segment:

Endpoint 1: (5, 7)

Endpoint 2: (-2, -7)

The complex number corresponding to each point:

Endpoint 1 corresponds to the complex number 5 + 7i.

Endpoint 2 corresponds to the complex number -2 - 7i.

Now, let's find the complex number that is common to both lines, i.e., the intersection point of these lines. To find the intersection, we need to find where the equations representing these lines intersect, assuming they continue infinitely in both directions.

The equation of the line passing through two points
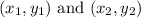`\((x_1, y_1)\) and \((x_2, y_2)\)` is given by:

`\[y - y_1 = \frac{{y_2 - y_1}}{{x_2 - x_1}} (x - x_1)\]`

Let's find the intersection point of the lines formed by these complex numbers:

For the first line:

`\[\frac{{-4 - 3}}{{4 - (-3)}} = \frac{{-7}}{{7}} = -1\]`

So, the equation for the first line segment is y = -x.

For the second line:

`\[\frac{{-7 - 7}}{{-2 - 5}} = \frac{{-14}}{{-7}} = 2\]`

So, the equation for the second line segment is y = 2x + 17.

To find the common complex number (intersection point), we need to solve these equations simultaneously:

y = -x

y = 2x + 17

Solving these equations, we find x = -17/3 and y = 17/3.

Therefore, the common complex number to both lines is -17/3 + 17i/3.

Answer 2

Problem Statement

The question gives us a graph of two lines and we are told that the lines have endpoints thta represent complex numbers. We are asked to find:

1. The pairs of complex numbers.

2. The complex number common to both lines.

Method

- To solve the question, we must first understand what the graph describes. The graph is NOT an ordinary real-line graph but rather a complex number graph showing the imaginary part on the y-axis and the real part on the x-axis.

- This means that the coordinate of the points on the graph is a coordinate of real and imaginary part. For example: