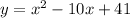Question

The vertex form of the equation of a parabola is y=(x-5)2+16.What is the standard form of the equation?

a. y=x2-10x+41
b. y=x2+10x+16
c. y=x2+x+8
d. y=3x2-10x+41

Answer 1

`y=(x-5)^2+16 \\ y=x^2-2 * x * 5+5^2+16 \\ y=x^2-10x+25+16 \\ y=x^2-10x+41`

The answer is A.

Answer 2

Option (A) is correct.

The standard form of the equation of parabola
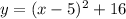`y=(x-5)^2+16` is
`y=x^2-10x+41`

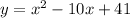
Explanation:

Given : The equation of a parabola is
`y=(x-5)^2+16`

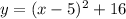
We have to find the standard form of the equation of parabola

Consider the equation of a parabola is
`y=(x-5)^2+16`

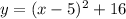
Applying algebraic identity
`(a-b)^2=a^2+b^2-2ab`

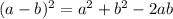
We have, a= x and b = 5

`(x-5)^2=x^2+5^2-2\cdot x\cdot 5`

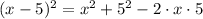
Simplify, we have,

`(x-5)^2=x^2-10x+25`

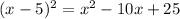
Substitue, we have,

`y=x^2-10x+25+16`

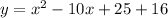
Simplify, we have,

`y=x^2-10x+41`

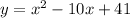
Thus, The standard form of the equation of parabola
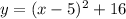`y=(x-5)^2+16` is
`y=x^2-10x+41`