Question

What is the general form of the equation of a circle with center at (a,

b. and radius of length m?
a. x2 + y2 − 2ax − 2by + (a2 + b2 − m2) = 0
b. x2 + y2 + 2ax + 2by + (a2 + b2 − m2) = 0
c. x2 + y2 − 2ax − 2by + (a + b − m2) = 0
d. x2 + y2 + 2ax + 2by + a2 + b2 = -m2

Answer 1

Answer is A just got it right on plato

Explanation:

Answer 2

This question is literally just about knowing your formulas.

The standard form equation is


`(x-a)^2+(y-b)^2=m^2`

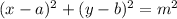
This is developed from the Pythagorean theorem. You can form a right triangle with some point on the circle (x, y) and its center (a, b). The legs will be the difference between x & a and y & b. The hypotenuse is the circle's radius. Plug this into the Pythagorean formula and this is what you get.
(also: no absolute value bars around the differences because any negative value will become positive when squared anyways)

To get this into general form, we could just distribute everything out and get it onto one side.

(x-a)² = x² - 2ax + a²
(y-b)² = y² - 2by + b²

Move the m² onto the right side, get everything ordered and...


`\boxed{x^2+y^2-2ax-2by+a^2+b^2-m^2=0}`

This looks most like our answer A. The parentheses aren't necessary because we can do addition/subtraction in any order, though.

Extra note: (h, k) is typically used for the center, and r is used for the radius.