Question

Two friends, Bob and Ben, each buy one lottery ticket. Each ticket contains six numbers from a total of one hundred numbers (0–99). Bob chooses the numbers 1, 2, 3, 4, 5, 6, and Ben chooses the numbers 39, 45, 66, 72, 74, 89. Who has a higher probability of winning?

Answer 1

both have equal chance

Answer 2

Answer: Bob and Ben, both have equal probabilities of winning.

Step-by-step explanation: Given that Bob and Ben are two friends who buy one lottery ticket each. Each ticket contains six numbers from a total of one hundred numbers from 0 to 99.

Bob chooses the numbers 1, 2, 3, 4, 5, 6, and Ben chooses the numbers 39, 45, 66, 72, 74, 89.

We are to select the friend who has a higher probability of winning.

Let, 'S' be the sample space for the experiment.

Then, S = {0, 1, 2, . . . , 98, 99} ⇒ n(S) = 100.

Let, B and F are the events that Bob win and Ben win respectively.

Then,

B = {1, 2, 3, 4, 5, 6} ⇒ n(B) = 6

and

F = {39, 45, 66, 72, 74, 89} ⇒ n(F) = 6.

Therefore, the probability of even t B is

`P(B)=(n(B))/(n(S))=(6)/(100)=6\%,`

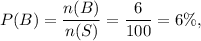
and the probability of event F is

`P(F)=(n(F))/(n(S))=(6)/(100)=6\%.`

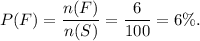
Since, both the events have equal probabilities, so there is an equal chance of winning of Bob and Ben.

Thus, both the friends have equal probabilities of winning.