Question

Widget wonders produces widgets. they have found that the cost, c(x), of making x widgets is a quadratic function in terms of x.....the company also discovered that it costs $103. to produce 3 widgets, $163 to produce 7 widgets, and $328 to produce 12 find the total cost of producing 2 widgets

Answer 1

It's quadratic function, so c(x) = ax^2 + bx + c. We know, that:

c(3) = 103 => 3^2 a + 3b +c = 103 => 9a+3b+c=103 (1)
c(7) = 163 => 7^2 a + 7b + c = 163 => 49a+7b+c=163 (2)
c(12)=328 => 12^2 a + 12b + c = 328 => 144a+12b+c=328 (3)

From first equation you get c = 103 - 9a - 3b
From second equation you get c = 163 - 49a - 7b
That's mean
103 - 9a - 3b = 163 - 49a - 7b
40a+4b=60 |:4
10a+b=15 => b = 15 - 10a

Substitute now c = 103 - 9a - 3b to third equation. You get
144a+12b+103-9a-3b=328
135a+9b=225 |:9
15a+b=25
b=25-15a

If b=15-10a and b=25-15a that's mean

15-10a=25-15a
5a=10 |:5
a=2

b=25-15a=25 - 15*2=25-30 = -5

c= 103 - 9a - 3b = 103 - 9*2 - 3*(-5)=103-18+15=100

You get the function:


`c(x)=2x^2-5x+100 \\ \\ \hbox{You have to find c(2):} \\ \\ c(2) =2 \cdot 2^2 - 5 \cdot 2 + 100 = 8-10+100=98`

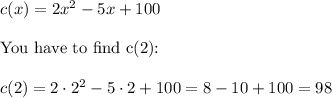
Answer: Total cost of producing 2 widgets is $98