Answer: The required probability that no girls and 3 boys will be chosen is

Step-by-step explanation: Given that a family has 8 girls and 4 boys. a total of 3 children must be chosen to speak on behalf of their family at a local benefit.
We are to find the probability that no girls and 3 boys will be chosen.
Let, S denotes the sample space for the experiment of choosing 3 children and E be the event that no girls and 3 boys will be chosen.
Then, we have
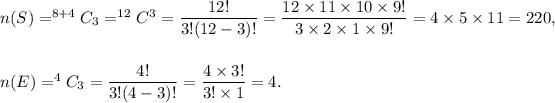
Therefore, the probability of event E will be
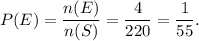
Thus, the required probability that no girls and 3 boys will be chosen is
