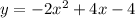Question

Find a quadratic model for the set of values: (-2, -20), (0, -4), (4,-20) Show your work

Answer 1

A quadratic function:

`y=ax^2+bx+c`

First, take the point (0,-4) and plug the values (x,y) into the equation:

`-4=a * 0^2+b * 0 +c \\ -4=c`

So the equation is
`y=ax^2+bx-4`.

Now plug the values of the other two points into the equation and set up a system of equation:

`-20=a * (-2)^2+b * (-2)-4 \\ -20=a * 4^2+b * 4-4 \\ \\ -20+4=4a-2b \\ -20+4=16a+4b \\ \\ -16=4a-2b \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ | / 2 \\ -16=16a+4b \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ |/ 4 \\ \\ -8=2a-b \\ \underline{-4=4a+b} \\ -12=6a \\ (-12)/(6)=a \\ a=-2 \\ \\ -8=2a-b \\ -8=2 * (-2)-b \\ -8=-4-b \\ -8+4=-b \\ -4=-b \\ b=4`

The function is:

`\boxed{y=-2x^2+4x-4}`

Answer 2

For this case, the quadratic function in its generic form is given by:

`image`

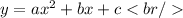
We must find the values of the coefficients.

For this, we evaluate the given points.

For (0, -4):

`image`

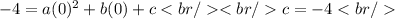
For (-2, -20):

`image`

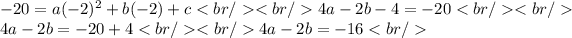
For (4, -20):

`image`

Therefore, for the values of a and b we have the following system of equations:

`image`

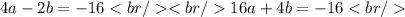
Resolving graphically (see attached image) we have:

`image`

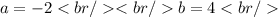
Then, the quadratic model is:

`image`

Answer:

a quadratic model for the set of values is:

`y = -2x ^ 2 + 4x - 4`