Let A be the amount of mix that contains 21% cashews and B the amount of mix that contains 16% cashews that will be used to create a mix with 19% cashews.
The total amount of mix will be A+B.
Notice that the total amount of cashews on that mix will be equal to:
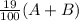
On the other hand, the total amount of cashews on the 21% mix, is:
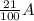
While the total amount of cashews on the 16% mix, is:
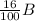
Then:
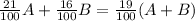
On the other hand, since the total amount of mix will be 74 pounds, then:
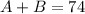
These two equations form a 2x2 system of equations. Solve the sistem to find A and B.
Isolate A from the first equation and substitute the expression into the second equation:
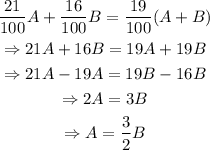
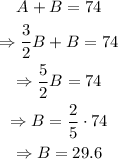
Substitute the value of B into the expression of A to find A:
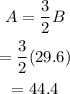
Therefore, 44.4 pounds of 21% cashews mix and 29.6 pounds of 16% cashews mix should be used to produce 74 pounds of 19% cashews mix.