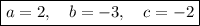Question

Give the values of a, b, and c from the general form of the equation (2x + 1)(x - 2) = 0.

Answer 1

a = 2, b = -3, c = -2

Explanation:

I just took the test, but give it to the other guy, he deserves it.

-sweety<3

Answer 2

When we expand this expression, we'll have a quadratic equation in the general form.

The general form of quadratic equations looks like this :


`a{ x }^( 2 )+bx+c\quad =\quad 0`

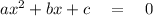
( a is coefficent of
`x^(2)` , b is coefficient of x and c is the constant)

So let's expand the expression.


`(2x+1)\cdot (x-2)\quad =\quad 0\\ \\ (2x\cdot x)+(2x\cdot -2)+(1\cdot x)+(1\cdot -2)\quad =\quad 0\\ \\ 2{ x }^( 2 )+(-4x)+x-2\quad =\quad 0\\ \\ 2{ x }^( 2 )-4x+x-2\quad =\quad 0\\ \\ 2{ x }^( 2 )-3x-2\quad =\quad 0`

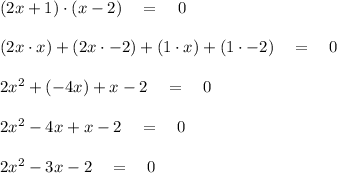
This how the final form of our equation :


`\boxed { 2{ x }^( 2 )-3x-2\quad =\quad 0 }`

As you can see
`x^(2)` 's coefficient (a) is 2 , x's coefficient (b) is -3 and the constant (c) is -2


`\boxed { a=2,\quad b=-3,\quad c=-2 }`