Question

In ∆ABC, AC = 15 centimeters, m B = 68°, and m C = 24°. What is BC to two decimal places?

6.58 centimeters
9.88 centimeters
13.57 centimeters
16.17 centimeters

Answer 1

The angles in a triangle add up to 180°, so m∠A=180°-(68°+24°)=180°-92°=88°.

Look at the picture.


`\sin 88^\circ = (h)/(15) \\ 0.9994 \approx (h)/(15) \\ 0.9994 * 15 \approx h \\ h \approx 14.991 \\ \\ \sin 68^\circ = (h)/(x) \\ 0.9272 \approx (14.991)/(x) \\ 0.9272x \approx 14.991 \\ x \approx (14.991)/(0.9272) \\ x \approx 16.17`

The answer is 16.17 cm.

Answer 2

16.17 centimeters

Explanation:

Let's take a look at the figure below:

We know that the sum of the angles in a triangle is 180º, so in order to find the measure of angle A, we would have:

A = 180 - 68 - 24

A = 88

Now we have all three angles and the measure of one side and we're required the length of side BC, to find this we can apply Law of Sines which states that:

`(a)/(sinA)=(b)/(sinB)  = (c)/(sinC)`

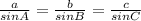
where A is the angle opposed to side a, and so on.

With the triangle given we have the side AC = 15 and its opposing angle B = 68. We need to find the side BC, and we know that its opposing angle is A = 88.

Writing this in Law of sines form and solving for BC we have:

`(15)/(sin68)=(BC)/(sin88)  \\BC = (15(sin88))/(sin68) \\BC=(15(0.9993))/(0.9272) \\BC= (14.9895)/(0.9272) \\BC= 16.166`

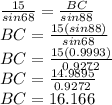
Therefore, BC = 16.166 ≈16.17 centimeters when rounded to two decimals.