Question

Write the equation of the line that passes through (–2, 6) and (2, 14) in slope-intercept form

Answer 1

Slope-intercept form is y = mx + b where m is the slope and b is the y-intercept. (the value of y when x = 0)

To find the slope, use the slope formula,
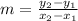
`m=(y_2-y_1)/(x_2-x_1)`, where (x¹, y¹) and (x², y²) are your two points.

For (-2, 6) and (2, 14):
`m=(14-6)/(2-(-2))=(8)/(2+2)=\frac84=2`

As a fraction, we would write the slope 2/1, but dividing by 1 is redundant when writing the actual equation.
Since slope is rise over run, we can interpret this slope as "when y changes by 2, x changes by 1 (and vice versa)"

Let's take one of our points, how about (-2, 6), and find our y-intercept from this.
We want to add 2 to x. According to our slope, this means adding 4 to y.
Our y-intercept is at (0, 10), with the value we put into our equation b = 10.

Final equation: y = 2x + 10