Question

Find all angles 0 theta such that 0 degrees is less than or equal to theta less than or equal to 360 degrees A) cos 0 = -square root of 3/2B) sin 0 = - square root of 2/2

Answer 1

A. 150 degrees and 210 degrees

B. 225 degrees and 315 degrees

EXPLANATION :

From the problem, we have :

`\begin{gathered} \cos\theta=-(√(3))/(2) \\ \\ and \\ \\ \sin\theta=-(√(2))/(2) \end{gathered}`

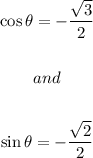
Note that the cosine of an angle is negative if the angle is in Quadrants II and III.

Reference angles are angles in the x-axis.

So we are looking for the angles when the cosine is negative.

Recall the identity :

`\cos30=(√(3))/(2)`

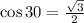
So we can say that the angle adjacent to the x-axis is 30 degrees.

The first angle (blue) is 180 less 30 degrees.

That's 180 - 30 = 150 degrees

The second angle (red) is 180 + 30 degrees.

That's 180 + 30 = 210 degrees

Therefore, we have :

A. 150 degrees and 210 degrees

For B, with the sine function :

The sine of an angle is negative if the angle is in Quadrants III and IV.

So we have angles on quadrants III and IV, of course, the angles are adjacent to the x-axis.

Recall the identity :

`\sin45=(√(2))/(2)`

So we can say that the angle is equal to 45 degrees.

The first angle (blue) is 180 + 45 degrees.

That's 225 degrees

The second angle is 360 less 45 degrees.

That's 360 - 45 = 315 degrees

So we have :

B. 225 degrees and 315 degrees