Question

Create an equation. Use the graph below to create the equation of the rainbow parabola.

Graph of a parabola opening down at the vertex 0 comma 36 crossing the x–axis at negative 6 comma 0 and 6 comma 0.
Create a table of values for a linear function. A drone is in the distance, flying upward in a straight line. It intersects the rainbow at two points. Choose the points where your drone intersects the parabola and create a table of at least four values for the function. Remember to include the two points of intersection in your table.

Answer 1

Remember that a quadratic with two real zeroes can be written as
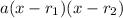
`a(x - r_1)(x - r_2)`, where
`a` is a constant and
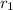
`r_1` and
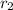
`r_2` are the zeroes (or roots) of the function. Since the graph shows that the two zeroes are at -6 and 6, the equation has to be of the form


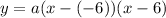
`y = a(x - ({-6}))(x - 6)`, or

`y = a(x + 6)(x - 6)`

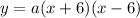
To solve for a, let's use the point at the vertex (0, 36) and plug that in:


`36 = a(0 + 6)(0 - 6)`

`36 = {-36}a`

`a = {-1}`
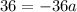
(It makes sense that
`a` is negative since the parabola opens down.)

So, the equation of the parabola is


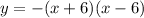
`y = -(x + 6)(x - 6)`, or

`\bf y = -x^2 + 36`

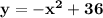
Now for the second part, just pick any two points with which we can draw a line with a positive slope. I'll use x = -2 and 1:


`y = -({-2})^2 + 36 = {-4} + 36 = 32`

`y = -(1)^2 + 36 = {-1} + 36 = 35`

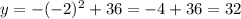
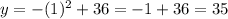
So, our two points are (-2, 32) and (1, 35). To find the equation of the linear function that goes through these two points, let's use slope-intercept form, which is
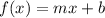
`f(x) = mx + b`. The slope
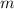
`m` is given by
`(y_2 - y_1)/(x_2 - x_1)`, so


`m = (y_2 - y_1)/(x_2 - x_1) = \frac{35 - 32}{1 - ({-2})} = 1`
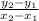
So, the equation of the linear function so far is just
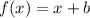
`f(x) = x + b`, and we can find
`b` by plugging in one of the points on the line:


`35 = 1 + b`

`b = 34`

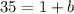
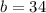
Thus, the equation of the linear function is


`\bf f(x) = x + 34`

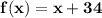
And you can find more points on the line simply by plugging other values of x, such as (0, 34) and (5, 39).