Question

Of the 1,000 students in a local college, 420 own brand X mobile phones and 580 own brand Y mobile phones. Of these students, 80 own both brands of mobile phones. Find the probability that a student chosen at random has a brand X mobile phone given that he has a brand Y mobile phone.

2/14

5/21

3/28

4/29

Answer 1

If we were to put this in terms of a venn diagram, we would have 360 owning only brand X, 500 owning only brand Y, and 80 in between, owning both. Therefore, 80 out of the 580 owners of brand Y may have X as well, which we put into fraction form 80/580, and reduce to 4/29.

Answer 2

Answer: The probability that a student chosen at random has a brand X mobile phone given that he has a brand Y mobile phone is 4/29.

Explanation:

Since, the total number of students, n(s) = 1,000

The number of students who have X mobile phones, n(X) = 420,

And, number of students who have Y mobile phones, n(Y) = 580,

Thus, the probability of the student that has Y phones,

`P(Y)=(n(Y))/(n(S))=(580)/(1000)=0.58`

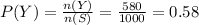
While, the number of students who have both phones, n(X∩Y) = 80

Thus, the probability of the student who has both phones,

`P(X\cap Y)=(n(X\cap Y))/(n(S))=(80)/(1000)=0.08`

Hence, the probability that a student chosen at random has a brand X mobile phone given that he has a brand Y mobile phone.

`P((X)/(Y))=(P(X\cap Y))/(P(Y))`

`=(0.08)/(0.58)`

`=(8)/(58)=(4)/(29)`

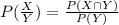
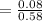
Hence, the required probability is 4/29.