Answer: The correct option is (b)
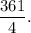
Step-by-step explanation: We are given to select the correct value of 'n' such that
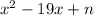 becomes a perfect square trinomial.
becomes a perfect square trinomial.
The standard form of a perfect square trinomial is
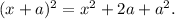
Now, we can write
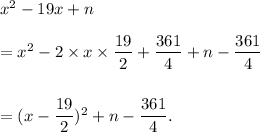
So, for the given expression to be perfect trinomial,
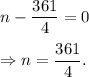
Thus, (b) is the correct option.