Question

Need help and explain please!!

Answer 1

`x=-4\text{ and } x=3`

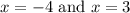
Explanation:

We are given the second derivative:

`g''(x)=(x-3)^2(x+4)(x-6)`

And we want to find its inflection points.

To do so, we will first determine possible inflection points. These occur whenever g''(x) = 0 or is undefined.

Next, we will test values for the intervals. Inflection points occur if and only if the sign changes before and after the point.

So first, finding the zeros, we see that:

`0=(x-3)^2(x+4)(x-6)\Rightarrow x=-4, 3, 6`

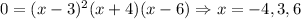
So, we can draw the following number-line:

<----(-4)--------------(3)----(6)---->

Now, we will test values for the intervals x < -4, -4 < x < 3, 3 < x < 6, and x > 6.

Testing for x < -4, we can use -5. So:

`g^\prime^\prime(-5)=(-5-3)^2(-5+4)(-5-6)=704>0`

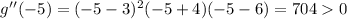
Since we acquired a positive result, g(x) is concave up for x < -4.

For -4 < x < 3, we can use 0. So:

`g^\prime^\prime(0)=(0-3)^2(0+4)(0-6)=-216<0`

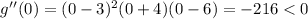
Since we acquired a negative result, g(x) is concave down for -4 < x < 3.

And since the sign changed before and after the possible inflection point at x = -4, x = -4 is indeed an inflection point.

For 3 < x < 6, we can use 4. So:

`g^\prime^\prime(4)=(4-3)^2(4+4)(4-6)=-16<0`

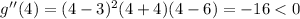
Since we acquired a negative result, g(x) is concave down for 3 < x < 6.

Since the sign didn't change before and after the possible inflection point at x = 3 (it stayed negative both times), x = -3 is not a inflection point.

And finally, for x > 6, we can use 7. So:

`g^\prime^\prime(7)=(7-3)^2(7+4)(7-6)=176>0`

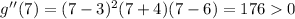
So, g(x) is concave up for x > 6.

And since we changed signs before and after the inflection point at x = 6, x = 6 is indeed an inflection point.