Question

The function f(x) = 2x2 + 3x + 5, when evaluated, gives a value of 19. What is the function’s input value?

Answer 1

`f(x)=\quad 2{ x }^( 2 )+3x+5`

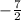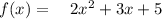
Let's called the input 'z'

When we plug 'z' in the function we get ;


`f(z)=\quad 2{ z }^( 2 )+3z+5`

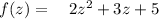
And we know that, this is equal to 19, so ;


`2{ z }^( 2 )+3z+5=\quad 19`

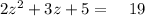
Let's rearrange the equation.


`2{ z }^( 2 )+3z+5=\quad 19\\ \\ 2{ z }^( 2 )+3z=\quad 19-5\\ \\ 2{ z }^( 2 )+3z=\quad 14\\ \\ 2{ z }^( 2 )+3z-14=\quad 0`

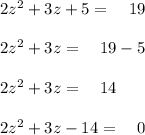
So we have a quadratic equation here.

We'll use this formula to solve it :


`\frac { -b\pm \sqrt { { b }^( 2 )-4ac } }{ 2a }`

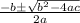
The formula is used in equation formed like this :


`a{ x }^( 2 )+bx+c=0`

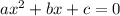
In our equation,

a=2 , b=3 and c=-14

Let's plug in the values in the formula to solve,


`a=2\quad b=3\quad c=-14\\ \\ \frac { -3\pm \sqrt { 9-(4\cdot 2\cdot -14) } }{ 4 } \\ \\ \frac { -3\pm \sqrt { 9-(-112) } }{ 4 } \\ \\ \frac { -3\pm \sqrt { 9+112 } }{ 4 } \\ \\ \frac { -3\pm \sqrt { 121 } }{ 4 } \\ \\ \frac { -3\pm 11 }{ 4 }`

So,


`z=\quad \frac { -3+11 }{ 4 } \quad ,\quad \frac { -3-11 }{ 4 } \\ \\ z=\quad \frac { 8 }{ 4 } \quad ,\quad \frac { -14 }{ 4 } \\ \\ z=\quad 2,\quad -\frac { 7 }{ 2 }`

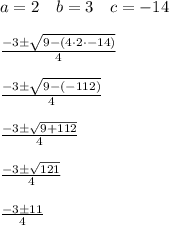
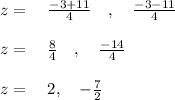
So the input can be both, 2 and
`-(7)/(2)`