Question

3^1/2 × a^2/3 × b^3/4
write as a single radical

Answer 1

remember rules of exponents

`x^{ (z)/(y) } = \sqrt[y]{x^(z)}`
combine because another rule is
√x times √y=√(xy) so

if we can make the denomenator of all fractions the same, then we can have a common root so
2 3 and 4
common number is 12 so
convert bottom number to 12 so
1/2=6/12



2/3=8/12


3/4=9/12


so the equation is


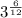
`3^{ (6)/(12) }` times
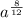
`a^{ (8)/(12) }` times
`b^{ (9)/(12) }`
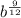
this equals


`\sqrt[12]{3^(6)}` times
`\sqrt[12]{a^(8)}` times
`\sqrt[12]{b^(9)}`

since we can combine we get

`\sqrt[12]{ 3^(6) a^(8) b^(9) }`