Answer:
the vertex represents a maximum
Vertex is (4,7)
f(x)=-(x-4)^2+7
Explanation:
Given the function
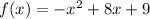
Equation is in the form of y=ax^2+bx+c

When 'a' is negative, then vertex is maximum
when 'a' is positive, then vertex is minimum
 is negative, so the vertex represents a maximum
is negative, so the vertex represents a maximum
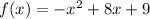 , factor out negative
, factor out negative
Take out negative sign in common