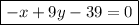Question

Write an equation of the line passing through (-3,4) and (6,5) and give the answer in standard form

Answer 1

Let's start by putting it into slope-intercept form, which is
y=mx+b where m=slope and b=y-intercept (the value of y when x=0)

Find the slope between (-3, 4) and (6, 5).
Formula for slope:
`m=(rise)/(run)=(y_2-y_1)/(x_2-x_1)`
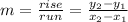
Plug in our x and y values...

`m=(5-4)/(6-(-3))=\frac{1}9`
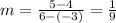
Our slope is 1/9.

We can interpret this slope rise/run = 1/9 as
"When y changes by 1, x changes by 9. (and vice versa)"
We want to find the y-intercept. (the value of y when x=0)
Let's take the point (-3, 4).
We want to add 3 to that x to make it 0.
According to our slope, this means adding 1/3 to y. (1 to 9 = 1/3 to 3)
Our y-intercept is at (0, 4 1/3), with the value we use in our eqn. b = 4 1/3.
Let's use an improper fraction, b = 13/3.

Now our equation is
`y=\frac{1}9x+\frac{13}3`
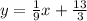
Let's convert to standard form, ax+by+c=0.
Just multiply by the LCD of our fractions (in this case, 9)

`9y=x+39`
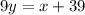
Now move everything to the left side.

`\boxed{-x+9y-39=0}`