Answer:
The number of ways to choose a set of 9 pencils from a selection of 10 is 10.
Explanation:
According to the combination formula, the total number of ways to select r items from total n items is
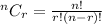
Total number of pencils = n = 10
Number of selected pencils = r = 9
The number of ways to choose a set of 9 pencils from a selection of 10 is
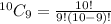

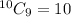
Therefore the number of ways to choose a set of 9 pencils from a selection of 10 is 10.