Question

Calculate the acceleration of a train that is traveling at a speed of 75 km/h and comes to a complete stop in 7 min. Dont forget the units.

Answer 1

`\begin{equation*} 642.9\text{ }(km)/(hour^2) \end{equation*}`

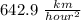
Step-by-step explanation

acceleration is is the rate of change in velocity over time, we can find it by using the formula

`\begin{gathered} a=(\Delta velocity)/(\Delta time)=\frac{v_f-v_o}{time\text{ taken}} \\ where \\ v_fis\text{ the final speed} \\ v_o\text{ is the initial speed} \end{gathered}`

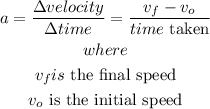
so

Step 1

a)Let

`\begin{gathered} initial\text{ speed=v}_o=75\text{ }(km)/(h) \\ final\text{ speed =v}_f=0(complete\text{ stop\rparen} \\ time=7\text{ minutes} \end{gathered}`

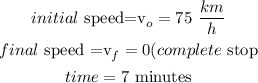
b) as the speed is given in km per hour, we need to convert the given time from minutes into hours,

so

`\begin{gathered} 1\text{ hour =}60\text{ minutes} \\ (1hour)/(60minutes) \\ so \\ 7\text{ minutes*}\frac{1\text{ hour}}{60\text{ minutes}}=0.116\text{ hours} \end{gathered}`

so

time=0.116 hours

Step 2

now we can replace the values in the formula

`\begin{gathered} a=\frac{v_(f)-v_(o)}{t\imaginaryI me\text{taken}} \\ a=\frac{0-75(km)/(h)}{0.116\text{ hours}}=-642.9\text{ }(km)/(hour^2) \end{gathered}`

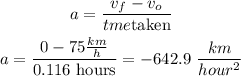
therefore, the acceleration is

`\begin{equation*} 642.9\text{ }(km)/(hour^2) \end{equation*}`

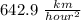
the negative sign indicates the acceleration is agains the motion.

I hope this helps you