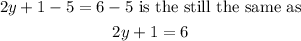Question

How can we find different ways to present algebraic equations without changing their meaning

Answer 1

There are different ways to present algebraic equations without changing their meaning. One way is to rearrange the terms of the equation using the properties of equality. Another way is to solve for a different variable in the equation.

Step-by-step explanation:

There are different ways to present algebraic equations without changing their meaning. One way is to rearrange the terms of the equation using the properties of equality. For example, if you have the equation 2x + 3 = 7, you can subtract 3 from both sides to get 2x = 4. Another way is to solve for a different variable in the equation. For example, if you have the equation 2x + 3y = 7, you can solve for y in terms of x by subtracting 2x from both sides and dividing by 3: y = (7 -2x)/3. These different ways of presenting the equations are equivalent and preserve the meaning of the original equation.

Answer 2

The Solution.

An Algebraic Equation can be defined as a mathematical statement that involves the following:

i. At least a letter ( an unknown)

ii. At least a number

iii. And an equality sign (i.e =)

An algebraic equation can be presented in any of the following ways without changing its meaning:

1. When you interchange an equation. For example, supoose the original equation is 2y+1 =6, when interchanged we get, 6=2y+1

So, 2y+1=6 has the same meaning as 6=2y+1

2. When you multiply through an initial equation by a positive or negative quantity( that is, mltiply both sides by a quantity). For example,

2y+1=6 has the same meaning as 2(2y+1)=2(6)

3. When you divide both sides of an equation by a quantity, the initial equation remain unchanged. For example,

`\begin{gathered} ((2y+1))/(4)=(6)/(4)\text{ is the same as} \\ \\ 2y+1=6 \end{gathered}`

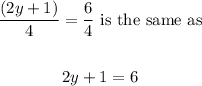
4. If you add or subtract same quantity from both sides, the initial equation still remains the same. For example,

`\begin{gathered} 2y+1-5=6-5\text{ is the still the same as} \\ 2y+1=6 \end{gathered}`