Question

3. In the two triangles pictured to theright: m(ZA) m(D) andm(LB) m(2E). Using a sequence oftranslations, rotations, reflections,andlor dilations, show that ABC issimilar to ADEF.

Answer 1

It is important to know that two triangles are similar if their corresponding interior angles are congruent. So, if we have two pairs of corresponding angles congruent, then we can prove that the third angle is also congruent.

`\begin{gathered} A+B+C=180 \\ D+E+F=180\rightarrow A+B+C=D+E+F\rightarrow\therefore C=F \end{gathered}`

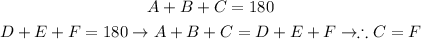
Given that all three interior angles are congruent between the triangles, then we can deduct that the triangles are actually similar.

On the other hand, using transformations, we would need to slightly rotate triangle ABC in a counterclockwise direction. Then, we would need to translate the triangle to the right side and then up. At last, the final transformation would be the dilation of a certain factor. That way we would prove graphically that the triangles are similar.