Question

THE LIFETIME OF A BATTERY USED IN A SMOKE ALARM IS NORMALLY DISTRIBUTED WITH A MEAN OF 4,000 HOURS AN A STANDARD DEVIATION OF 600 A. FIND THE % OF BATTERIES THAT WILL LAST BETWEEN 4120 AND 4720 HOURS? B.IF 500,000 BATTERIES ARE PRODUCED HOW MANY WILL LAST UP TO 4600 HOURS?

Answer 1

A) 30.6%

B) 420,500 batteries

Explanations:

A) First, we need to convert the range of number of hours to z-scores, this can be expressed as:

`z=\frac{x-\overline{\mu}}{\sigma}`

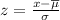
where

µ is the mean value

σ is the standard deviation

If the number of hours is 4120 hours, then the z-score will be;

`\begin{gathered} z_1=(4120-4000)/(600) \\ z_1=(120)/(600) \\ z_1=0.2 \end{gathered}`

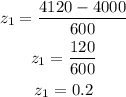
If the number of hour is 4720 hours, then the z-score wil be;

`\begin{gathered} z_2=(4720-4000)/(600) \\ z_2=(702)/(600) \\ z_2=1.2 \end{gathered}`

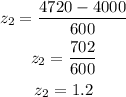
The equivalent z-score will be;

Such that;

`P(z<1)=0.8413=84.13\%`

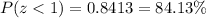
Find the required number of batteries

`\begin{gathered} Total\text{ batteries<}0.8413*500,000 \\ Total\text{ batteries}<420650batteries \\ Total\text{ batteries}=420,500 \\ \end{gathered}`

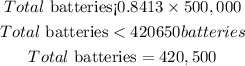
Since 420,500 is less than the calculated, hence the total batteries that will last up to 4600 hours is 420,500 batteries