Question

2. The height of a triangle is 5 m less than its base. The area of the triangle is 42 m2. Find the length of the base.

(Points : 1)

Answer 1

took the quiz and it is correct the answer is 12

Answer 2

Let's start with what we know

Area:

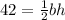
`42 = (1)/(2)bh` where 42 is the area, b = base, and h = height

Height:
Since we know the height is 5 less than the base, we can write that as an equation.

`h = b - 5`

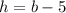
Now let's go and plug
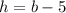
`h = b - 5` into
`42 = (1)/(2)bh`


`42 = (b)/(2)(b-5)`
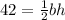
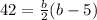
Let's distribute b over (b-5)


`42 = ( b^(2) - 5b )/(2)`
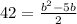
Let's move 42 over to the right side to make a quadratic formula


`0 = (1)/(2) b^(2) - (5)/(2)b - 42`

Let's plug that into the quadratic equation, which is:


`\frac{-b +/- \sqrt{ b^(2) - 4ac } }{2a}`
And we can now plug the pieces in to calculate b


`\frac{- (-(5)/(2)) +/- \sqrt{ (-(5)/(2))^(2) - 4 ((1)/(2))(-42) } }{2 ((1)/(2)) }`

`\frac{(5)/(2) +/- \sqrt{ (25)/(4) +84 } }{1 }`

`{(5)/(2) +/- \sqrt{ (361)/(4) } }`

`{(5)/(2) +/- { (19)/(2) }`
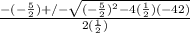
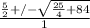
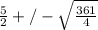
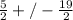
Since we can't have a negative value for b (a base can't be negative meters), let's add:


`{(5)/(2) + { (19)/(2) }`

`{ (24)/(2) }`

`12 = b`

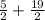
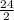
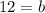
So the base of the triangle is 12m