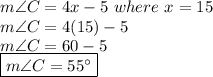In any statement like this one:
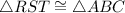
you can assume that the points match up in the order that you are given them.
This means that

.
We know that
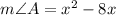
and
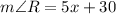
, and because they are congruent we can set the two equal to each other.
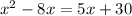
Let's get everything to one side.
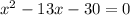
Let's solve by factoring, since it's easy to do with these whole numbers.
We're looking for two number thats add to -30 and multiply to -13...
These would be -15 and 2.
Since our leading coefficient (_x²) is 1, we can factor straight to (x-15)(x+2).
Here's what it would look like if you went through all the steps anyways, though.
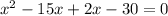

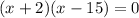
Any value which causes either factor to equal 0 is a solution.
(The second factor wouldn't matter b/c 0 times anything is still 0)
Therefore x = -2 or 15.
Only one of these is possible, however!
If you use x = -2, you will find that the angle measure 4x-5 is negative, which is impossible. In this case, x must be 15.
Let's find the measure of angle C.