Question

The width,w, of a rectangular garden is X -2 the area of the garden is X^3-2X-4 what is an expression for the length of the garden?

A. X^2-2x-2
B. X^2+2x-2
C. X^2-2x+2
D. X^2+2x+2

Answer 1

`A=lw \Rightarrow l=(A)/(w)`
A - area, l - length, w - width


`w=x-2 \\ A=x^3-2x-4 \\ \\ l=(x^3-2x-4)/(x-2)=(x^3-2x^2+2x^2-4x+2x-4)/(x-2)=(x^2(x-2)+2x(x-2)+2(x-2))/(x-2)= \\ =((x^2+2x+2)(x-2))/(x-2)=x^2+2x+2`

The answer is D. x²+2x+2.

Answer 2

D.
`x^2+2x+2`

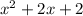
Explanation:

We know that,

The area of a rectangle is,

A = l × b,

Where, l is the length of the rectangle,

w is the width of the rectangle,

Given,

`A = x^3-2x-4`

`w=(x-2)`

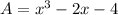
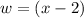
By substituting values,

`x^3-2x-4=(x-2)l`

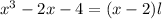
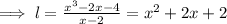`\implies l = (x^3-2x-4)/(x-2)=x^2+2x+2` ( By long division shown below )

Hence, the length of the rectangular garden is
`x^2+2x+2`

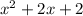
Option D is correct.