Question

49 After decaying for 48 hours, l/16 of the original mass of a radioisotope sample remains unchanged. What is the half-life of this radioisotope?

(1) 3.0 h (3) 12 h(2) 9.6 h (4) 24 h

Answer 1

1/16 left would imply 4 half lives have passed (1/2 left = 1, 1/4 left = 2, 1/8 left = 3, 1/16 left = 4). So 4 half lives passed in 48 hours, meaning dividing 48 by 4 will give you the length of 1 half life. Which in this case is 12 hours.

Answer 2

The half life of the radioisotope is 12 hours.

Step-by-step explanation:

Initial mass of the radioisotope = x

Final mass of the radioisotope =
`(1)/(16)* x` = 0.0625x

Half life of the radioisotope =
`t_{(1)/(2)}`

Age of the radioisotope = t = 48 hours

Formula used :

`N=N_o* e^(-\lambda t)\\\\\lambda =\frac{0.693}{t_{(1)/(2)}}`

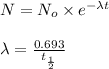
where,

`N_o` = initial mass of isotope

N = mass of the parent isotope left after the time, (t)

`t_{(1)/(2)}` = half life of the isotope

`\lambda` = rate constant

`N=N_o* e^{-((0.693)/(t_(1/2)))* t}`

Now put all the given values in this formula, we get

`0.0625x=x* e^{-((0.693)/(t_(1/2)))* 48 h}`

`\ln(0.0625) * (1)/((-0.693* 48 h))=(1)/(t_(1/2))`

`t_(1/2) = 11.99 hours = 12 hours`

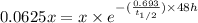
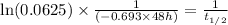
The half life of the radioisotope is 12 hours.