Question

paanshte the worles, as or symmetey and minimax value of each 2 = 2x2-8X-3convert to vertex form .indentify the vertex, axis of symmetry, min/max ,y-intercept and then graph- the instructions and the problem y =2(x-3) squareed +1

Answer 1

The equation is,

`y=2(x-3)^2+1`

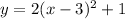
The general equation of parabola with vertex (h,k) is,

`y=a(x-h)^2+k`

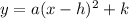
On compare the equation of parabola with general equation, the values are a = 2, h = 3 and k = 1 , the vertex of parabola is (h,k). So vertex of parabola is (3,1).

The value of a is more than 0, means parabola open upward so vertex correspond the minimum value. Minimum value is 1 for x = 3.

The parabola vertex is (3,1) and axis of symmetry for parabola is x = h. So axis of symmetry is x = 3.

Substitute 0 for x in equation to obtain the y-intercept of function.

`\begin{gathered} y=2(0-3)^2+1 \\ =18+1 \\ =19 \end{gathered}`

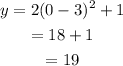
So y-intercept is (0,19).

Plot the equation on the graph.