Question

If you know that the period of a pendulum is 1.87 seconds, what is the length of that pendulum? (Assume that we are on Earth and that gravity is 9.81 meters/second².) Select one of the options below as your answer: A. 0.87 centimeters B. 2.1 meters C. 1.6 meters D. 0.87 meters E. 8.3 meters

Answer 1

Period of an ideal simple pendulum = 2π √(L / G)

1.87 = 2π √ (L / 9.81)

Divide each side by 2π : (1.87 / 2π) = √ (L / 9.81)

Square each side: (1.87 / 2π)² = L / 9.81

Multiply each side by 9.81 : L = (9.81) (1.87 / 2π)² = 0.869 meter

Choice 'D' is the closest one.

Answer 2

Answer : The correct option is, (D) 0.87 meters

Solution :

Formula used :

`T=2\pi * \sqrt{(L)/(g)}`

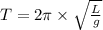
where,

T = time period of a pendulum = 1.87 seconds

L = length of the pendulum = ?

g = gravity on earth =
`9.8m/s^2`

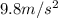
Now put all the given values in the above formula, we get the length of the pendulum.

`1.87s=2* (22)/(7)* \sqrt{(L)/(9.8m/s^2)}`

`0.2975=\sqrt{(L)/(9.8m/s^2)}`

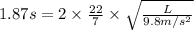
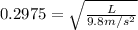
Now squaring on both the sides, we get

`L=0.868m=0.87m`

Therefore, the length of the pendulum is, 0.87 meters.