Question

If sin theta = (sqrt 3)/2, which could not be the value of theta? A. 60 degrees B. 120 degrees C. 240 degrees D. 420 degrees I know that the solutions for theta are pi/3 and 2pi/3, but how does that correlate?

Answer 1

Your are right,
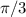
`\pi /3` and 2
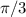
`\pi /3` are solutions.
Of course each of these solutions can be replaced by the same number +k2
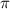
`\pi` (with k being an element of Z) since sin x=sin (x+k2
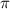
`\pi`) with k being an element of Z.
Those are angle measures expressed in radians.
If you translate in degrees you basically have to know that
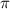
`\pi` radian=180 degrees
so
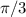
`\pi /3` radian=60 degrees and 2
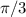
`\pi /3`=120 degrees. So this two could be values of theta (A and B).
On top of that
`\pi /3+2 \pi` could also be a solution (x+k2
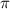
`\pi` with k=1). This can be translated to 60+360=420 degrees which is solution D.
So C. 240 degrees is the only one that could not be a value of theta.