Question

the graph of f(x)=x is shown on the cooridinate plane. function g is a transformation of f as shown below. g(x)=f(x-5)

Answer 1

For this exercise you need to remember the following Transformation rules for for a function f(x):

1) If:

`f(x-h)`

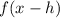
Then the function is shifted right "h" units.

2) If:

`f(x+h)`

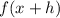
Then the function is shifted left "h" units.

In this case you have this parent function:

`f(x)=x`

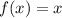
Which is a line that passes through the point (0,0) or "The origin".

You know that the function g(x) is a transformation of f(x), and this is:

`g\mleft(x\mright)=f\mleft(x-5\mright)​`

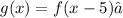
So you can identify that the transformation has the form:

`f(x-h)`

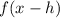
Where:

`h=5`

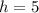
Therefore, the graph of g(x) is the graph of f(x) but shifted right 5 units.

Then, the graph of the function g(x) is: