Question

?pounds of the alloy containing 34% copper?pounds of the alloy containing 48% copper

Answer 1

He has to combine two alloys to obtain 46 pounds of a 37%-copper alloy.

The first alloy (x) contains 34% copper, while the second alloy (y) contains 48% copper.

The variables x and y will represent the mass of the first and second alloy respectively.

Then, we start by writing that the sum of the mass of the two alloys has to be 46 pounts. Then we can write:

`x+y=46`

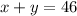
We need another equation, so we will look at the amount of copper.

The sum of the copper of the alloys has to be equal to the amount of copper of the blend.

The amount of copper of an alloy is equal to the mass times the proportion of copper of each alloy.

Then, we can write:

`\begin{gathered} x\cdot0.34+y\cdot0.48=46\cdot0.37 \\ 0.34x+0.48y=17.02 \end{gathered}`

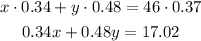
Now, we can replace y in the second equation, using the information from the first equation:

`\begin{gathered} x+y=46\Rightarrow y=46-x \\ \Rightarrow0.34x+0.48(46-x)=17.02 \\ 0.34x+0.48\cdot46-0.48x=17.02 \\ (0.34-0.48)x+22.08=17.02 \\ -0.14x=17.02-22.08 \\ -0.14x=-5.06 \\ x=(5.06)/(0.14) \\ x\approx36.14 \end{gathered}`

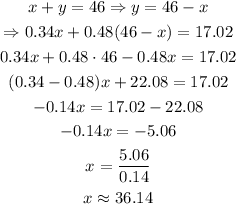
Now, with the value of x, we can find the value of y as:

`\begin{gathered} y=46-x \\ y\approx46-36.14 \\ y\approx9.86 \end{gathered}`

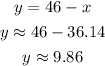
Answer: the blend can be made from 36.14 pounds of the 34%-copper alloy and 9.86 pounds of the 48%-copper alloy.