Question

Find all integers n for which n^2+6n-27 is a prime number? Please tell me how you did it.

Answer 1

`n^2+6n-27=\\ n^2-3n+9n-27=\\ n(n-3)+9(n-3)=\\ (n+9)(n-3)`
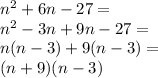
For the above product to be a prime number, one of the factors must be a prime number and the other must be equal to 1.


`n+9=1\\ n=-8\\\\ -8-3=-11`
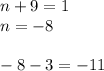
The first factor is equal 1 for
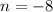
`n=-8`, but the other is euqal -11, which is not a prime number.


`n-3=1\\ n=4\\\\ 4+9=13`
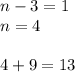
The second factor is equal 1 for
`n=4` and the first factor is equal 13, which is a prime number.

So,
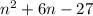
`n^2+6n-27` is a prime number for
`n=4`