Question

Flying against the wind, an airplane travels 4620km in 6 hours. Flying with the wind, the same plane travels 3750km in 3 hours. What is the rate of the plane in still air and what is the rate of the wind?

Answer 1

Let us call the rate as velocity. Now the velocities of the plane and of the wind are:

`v_(p)` and
`v_(w)`:
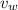
Now

case 1:
`v_(p) - v_(w) =4620/6=770 km/h`

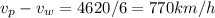
case 2:
`v_(p) + v_(w) =3750/3=1250 km/h`

from equation 2:
`v_(w) = 1250 - v_(p)`
substitute in equation 1:

`v_(p) - 1250 + v_(p) =770 v_(p) = 1010 km/h`
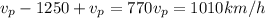
Which is your velocity in still air (without wind)
Substituting back in:

`v_(w) = 1250 - v_(p)`
you get:

`v_(w) = 1250-1010 = 240 km/h`
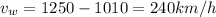
which is the wind velocity