Question

A balloon with an unknown gas at the surface of the ocean has a volume 2.5 L, a pressure of 1.0 atm and a temperature of 325.4 K. The balloon is submerged into the water to an unknown depth where the temperature drops to 275.9 K and the pressure increases to 293.4 kPa. What is the new volume in mL? (1000 mL = 1 L, 101.325 kPa = 1 atm).

Answer 1

1) List the known and unknown quantities.

Initial conditions

Volume: 2.5 L.

Pressure: 1.0 atm.

Temperature: 325.4 K.

Final conditions

Temperature: 275.9 K.

Pressure: 293.4 kPa.

Volume: unknown (mL).

2) Set the equation

The combined gas law.

`(P1V1)/(T1)=(P2V2)/(T2)`

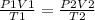
2.1- Convert kPa to atm.

101.325 kPa = 1 atm

`atm=293.4\text{ }kPa*\frac{1\text{ }atm}{101.325\text{ }kPa}=2.896\text{ }atm`

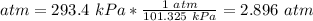
3) Plug in the known quantities

.

`\frac{(1.0\text{ }atm)(2.5\text{ }L)}{325.4\text{ }K}=\frac{(2.896\text{ }atm)(V2)}{275.9\text{ }K}`

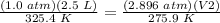
Multiply on both sides by 275.9 K.

`\frac{(1.0\text{ }atm)(2.5\text{ }L)}{325.4\text{ }K}*275.9\text{ }K=\frac{(2.896\text{ }atm)(V2)}{275.9\text{ }K}*275.9\text{ }K`

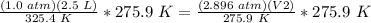
Divide both sides by 2.896 atm.

`\frac{(1.0\text{ }atm)(2.5\text{ }L)(275.9\text{ }K)}{325.4\text{ }K}*\frac{1}{2.896\text{ }atm}=\frac{(2.896atm)(V2)}{2.896\text{ }atm}`

.

`V2=\frac{(1.0\text{ }atm)(2.5\text{ }L)(275.9\text{ }K)}{(325.4\text{ }K)(2.896\text{ }atm)}`
`V2=0.73\text{ }L`

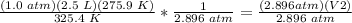
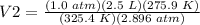
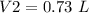
4) Convert L to mL.

1 L = 1000 mL

`mL=0.73\text{ }L*\frac{1000\text{ }mL}{1\text{ }L}=730\text{ }mL`

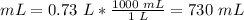
The final volume at the unknown depth is 730 mL.

.