x^2=4x-5
subtract 4x from both sides
x^2-4x=-5
add 5 to both sides
x^2-4x+5=0
input into quadratic formula which is x=
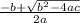
or
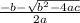
si ax^2+bx+c
so a=1
b=-4
c=5
input
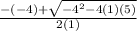
=
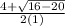
=
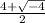
=

![(4+2 times √(-1) )/(2)= (6 times √(-1) )/(2)=3 times √(-1) [\tex][\tex]√(-1)](https://img.qammunity.org/2016/formulas/mathematics/middle-school/qu7nex16fidtshvsucsn4crbdobc4wwheg.png)
representeds by 'i' so solution is 3i
then if other way around then wyou would do
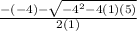
=
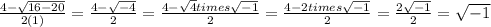
and [\tex]\sqrt{-1} [/tex] is represented by i
the solution is x=3i or i (i=

)
but i is not real, it is imaginary so there are no real solution so the answer is C