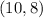Question

Evelyn has a nickels and y pennies. She has a maximum of 20 coins worth aminimum of $0.40 combined. Solve this system of inequalities graphically anddetermine one possible solution.

Answer 1

Let be "x" the number of nickels Evelyn has and "y" the number of pennies she has.

According to the information given in the exercise, she has a maximum of 20 coins. Then, you can set up the following inequality to represent it:

`x+y\le20`

Because "a maximum of 20 coins" indicates that the total number of coins is less than or equal to 20.

You also know that that money is worth a minimum of $0.40. Then, you can set up this inequality:

`0.05x+0.01y\ge0.40`

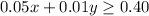
Since the first inequality is:

`x+y\le20`

You need to solve for "y" in order to rewrite it:

`y\le-x+20`

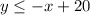
Knowing that the second inequality is:

`0.05x+0.01y\ge0.40`

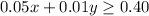
You can solve for "y" in order to rewrite it:

`\begin{gathered} 0.01y\ge-0.05x+0.40 \\ \\ y\ge(-0.05x)/(0.01)+(0.40)/(0.01) \\ \\ y\ge-5x+40 \end{gathered}`

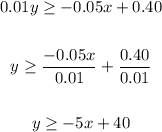
Therefore, the System of Inequalities is:

`\begin{cases}y\le-x+20 \\ y\ge-5x+40\end{cases}`

The Slope-Intercept Form of the equation of a line is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

- Notice that the first line of the system is:

`y=-x+20`

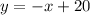
You can identify that:

`b_1=20`

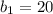
You can find the x-intercept by substituting the following value of "y" into the equation and solving for "x":

`y=0`

Then, you get:

`\begin{gathered} 0=-x+20 \\ x=20 \end{gathered}`

Therefore, you know that the first line passes through these points:

`(20,0);(0,20)`

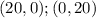
- Since the second line is:

`y=-5x+40`

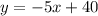
You can determine that:

`b_2=40`

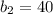
To find the x-intercept, apply the same procedure used for the first line:

`\begin{gathered} 0=-5x+40 \\ -40=-5x \\ \\ (-40)/(-5)=x \\ \\ x=8 \end{gathered}`

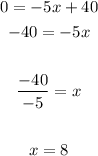
Then, the line passes through these points:

`(8,0);(0,40)`

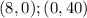
- Notice that the symbol of the first inequality is:

`\le`

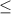
That indicates that the first line is solid and the shaded region must be below the line.

- The symbol of the second inequality is:

`\ge`

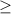
This indicates that the line is solid and the shaded region must be above the line.

Knowing the explained above, you can graph the System of Inequalities:

By definition, the solution of the System of Inequalities is the intersection region.

Then, in order to determine one possible solution, you can choose a point in the intersection region. This can be (the solution contains this point):

`(10,8)`

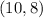
Therefore, answers are:

-Inequality 1:

`y\le-x+20`

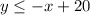
- Inequality 2:

`y\ge-5x+40`

- Graph:

- The solution contains this point:

`(10,8)`