Question

Could the points (-4,3), (-1,1) and (1,3) form the vertices of a right triangle? Why or why not?

Answer 1

`A=(-4,3),B=(-1,1),C=(1,3)\\ |AB|=√((-4+1)^2+(3-1)^2)=√(9+4)=√(13)\\ |BC|=√((-1-1)^2+(1-3)^2)=√(4+4)=√(8)\\ |AC|=√((-4-1)^2+(3-3)^2)=√(25+0)=5\\ L=√(13)^2+√(8)^2=13+8=21\\eq5^2\\eq\ R`

It's impossible to form right triangle using thes points.

Answer 2

The given points of triangle do not form a right triangle because they are satisfying the property of right angle triangle.

Explanation:

Given : The points (-4,3), (-1,1) and (1,3)

To find : Could the points form the vertices of a right triangle? Why or why not?

Solution :

First we find the distance between the points so that we get the length of the sides.

Let, A=(-4,3), B=(-1,1), C=(1,3)

Distance formula is

`d=√((x_1-x_2)^2+(y_1-y_2)^2)`

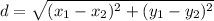
The distance between point A and B

`|AB|=√((-4+1)^2+(3-1)^2)=√(9+4)=√(13)`

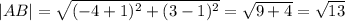
The distance between point B and C

`|BC|=√((-1-1)^2+(1-3)^2)=√(4+4)=√(8)`

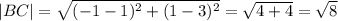
The distance between point A and C

`|AC|=√((-4-1)^2+(3-3)^2)=√(25+0)=5`

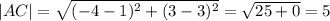
According to property of triangle,

If the square of larger side of triangle is equating to the sum of square of smaller side
`a^2=b^2+c^2` the triangle is right triangle .

Larger side of the triangle is AC=5 unit and smaller sides are
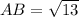`AB=√(13)` and
`BC=√(8)`

`AC^2=AB^2+BC^2`

`5^2=√(13)^2+√(8)^2`

`25=13+8`

`25\\eq21`

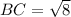
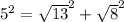
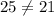
So, The given points or the vertices of triangle do not form a right triangle because they are satisfying the property of right angle triangle.