Question

Find in simplest radical form, the length of the line segment with endpoints whose coordinates are (-1,4) and (3,-2)?

Answer 1

The distance is
`2√(13)` units

Step-by-step explanation:

The distance between two points can be calculated using the following rule:

distance =
`\sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2}`

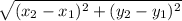
The given points are:

(-1,4) representing (x₁,y₁)

(3,-2) representing (x₂,y₂)

Substitute in the formula with the givens to get the distance as follows:

distance =
`√((3--1)^2+(-2-4)^2) = 2√(13)` units

Hope this helps :)

Answer 2

`d = \sqrt{(x_2 - x_1)^(2) + (y_2 - y_1)^(2)} \\d = \sqrt{(3 - (-1))^(2) + (-2 - 4)^(2)} \\d = \sqrt{(3 + 1)^(2) + (-6)^(2)} \\d = \sqrt{(4)^(2) + 36} \\d = √(16 + 36) \\d = √(52) \\d = 2√(13)`