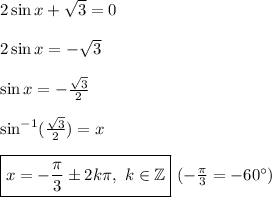Question

Solve 2sin x + sqrt3 = 0

Answer 1

Subtract sqrt 3 to isolate 2sin x
Divide by 2 to isolate sin x
Take the arcsin of each side to isolate x
Thinking of a 30-60-90 triangle, we know that x sqrt 3 is opposite 60° and 2x acts as the hypotenuse, thus it will be some variation of 60°.
In order to produce a negative result, x must be -60° (-π/3)
It is worth noting that this is a restricted value. Any addition/subtraction of 2π from this answer will produce the same result, thus your full answer is the above plus or minus 2kπ where k ∈ Z (k is an interger)


`2\sin x+√(3)=0\\\\2\sin x=-√(3)\\\\\sin x=-\frac{√(3)}2\\\\\sin^(-1)(\frac{√(3)}2)=x\\\\\boxed{x=-\frac{\pi}3\pm2k\pi,\ k\in \mathbb{Z}}\ (-\frac{\pi}3=-60\°)`