Answer:
∠A ≅ ∠A and ∠ABD ≅ ∠ACB, so ΔABD ≅ ΔACB by the AA (Angle - Angle) Triangle Similarity Theorem.
AB = 10
Step-by-step explanation:
An angle is congruent to itself, so ∠A ≅ ∠A
On the other hand, taking into account the representation of the angles, we can say that: ∠ABD ≅ ∠ACB
Then, the triangles ABD and ACB are congruent by the AA (Angle-Angle) triangle similarity theorem because we have two congruent angles:
∠A ≅ ∠A
∠ABD ≅ ∠ACB
Now, if two triangles are similar their corresponding sides are proportional.
So, we can formulate the following equation:
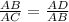
Then, replacing AC by (21 + 4), AD by 4, and solving for AB, we get:
![\begin{gathered} (AB)/(21+4)=(4)/(AB) \\ AB* AB=4(21+4) \\ AB^2=4(25) \\ AB^2=100 \\ AB=\sqrt[]{100} \\ AB=10 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/6b36b9nrzv20czht1uwg.png)
Therefore, the answers are:
∠A ≅ ∠A and ∠ABD ≅ ∠ACB, so ΔABD ≅ ΔACB by the AA (Angle - Angle) Triangle Similarity Theorem.
AB = 10