When a quadratic is in the form

, your min/max =

.
When a quadratic is in the form
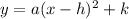
, your min/max =

.
Let's take a look at all of these answers.
1) y = x² + 16#1 in is general form. (y=ax²+bx+c)
a=1, b=0, c=16.

So we know that the min/max is 16. We don't know
which it is, though.
2) y = -x² + 16I've rearranged this equation to general form.
As you can see, this will have the same outcome as the previous, with the min/max being 16.
3) y = (x-16)²This is in y = (x-h)² + k form, but there is no k, thus the min/max k = 0.
This is also true for
4) y = (x+16)².
Let's go back to #1 and #2.
While vertex form
y = (x-h)² + k makes finding the vertex easy, it is a lot easier to know whether we have a minimum or a maximum in y =
ax² + by + c form.
Simply put: If a is positive, the parabola opens upwards and we have a min.
If a is negative, it opens downwards and we have a max.
We want a
maximum value of 16, so that means
negative a.
Thus our answer is
2) y = -x² + 16