Question

In ABC,X is the centroid if XZ=3, What is AZ

Answer 1

In every triangle, the centroid divides each segment starting through a vertex and passing through it (that is, the segments AZ, BY and CW) in two parts, where one part (starting from the vertex) is two times the other part.

So we have the following relations:

`\begin{gathered} AX=2\cdot XZ \\ CX=2\cdot XW \\ BX=2\cdot XY \end{gathered}`

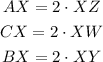
So using the value XZ = 3, we can find the value of AX:

`\begin{gathered} AX=2\cdot XZ \\ AX=2\cdot3 \\ AX=6 \end{gathered}`

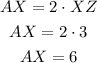
Then, since the segment AZ is the sum of the segments AX and XZ, we have:

`\begin{gathered} AZ=AX+XZ \\ AZ=6+3 \\ AZ=9 \end{gathered}`

So the length of AZ is equal 9.