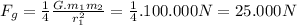Question

The Earth has a radius of 6,400 kilometers. A satellite orbits the Earth at a distance of 12,800 kilometers from the center of the Earth. If the weight of the satellite on Earth is 100 kilonewtons, the gravitational force on the satellite in orbit is?

It would be great if you could add a few words of explanation.

Answer 1

By using a universal gravitational force, we can get that
`F_(g) = (G. m_(1) . m_(2))/( r^(2) )`.

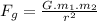
For note : r is a distance from center of the earth to the object.

Then, if
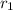
`r_(1)` is 6.400 km, and if
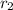
`r_(2)` is 12.800 km,
we can say that
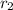
`r_(2)` is
`2r_(1)`

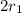
In first equation we can say that :

`F_(g) = (G.m_(1) m_(2) )/( r_(1)^(2) ) = 100.000 N`

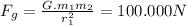
then in second equation we can say that :

`F_(g) = (G.m_(1) m_(2) )/( r_(2)^(2) )`,

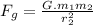
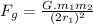
`F_(g) = (G.m_(1) m_(2) )/( (2r_(1))^(2) )` (because
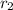
`r_(2)` is
`2r_(1)` )

`F_(g) = (G.m_(1) m_(2) )/( 4r_(1)^(2) )`,
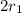
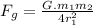
we can say that :
`F_(g) = (1)/(4) (G.m_(1) m_(2) )/( r_(1)^(2) )`
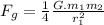
so, by plugging first equation into second equation, we can get

`F_(g) = (1)/(4) (G.m_(1) m_(2) )/( r_(1)^(2) ) = (1)/(4) . 100.000 N = 25.000 N`