Question

A car of mass 1,325 kg makes a circular turn of radius 16.18 m along a level roadway. The coefficient of friction is 0.826 between the tires and the road.How fast (in m/s) can the car go without skidding off the turn?(Use the approximation that g ≈ 10 m/s^2)Answer: ________ m/s (round to the nearest hundredth)

Answer 1

Given:

The mass of the car is,

`m=1325\text{ kg}`

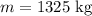
The radius of the circular path is,

`r=16.18\text{ m}`

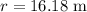
The coefficient of friction between the tires and the road is,

`\mu=0.826`

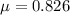
The acceleration due to gravity is,

`g=10\text{ m/s}^2`

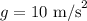
To find:

How fast (in m/s) can the car go without skidding off the turn

Step-by-step explanation:

The frictional force balances the centripetal force.

The frictional force is,

`f=\mu mg`

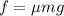
The centripetal force is,

`F=(mv^2)/(r)`

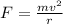
Here, v is the speed of the car without skidding.

We can write,

`\begin{gathered} (mv^2)/(r)=\mu mg \\ v=√(\mu gr) \end{gathered}`

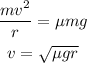
Substituting the values we get,

`\begin{gathered} v=√(0.826*10*16.18) \\ v=11.6\text{ m/s} \end{gathered}`

Hence, the required speed is 11.6 m/s.